Funktionen (Oberstufe)
Für jede selbständig gelöste Aufgabe bekommst du einen Punkt, für jeweils 50 Punkte einen Stern.
Aktueller Punktestand: 0
Hinweise zur Eingabe
- Notiere Brüche als Division (und kürze vorher!): 1/2; 1/3...
- Notiere Hochzahlen mit dem Dach-Symbol (falls keine Felder vordefiniert sind): x^n
- x² = x^2
- x³ = x^3
- Achte darauf, vordefinierte Felder richtig mit Vorzeichen und Variablen auszufüllen (siehe Beispiele)
Rechenregeln und Beispiele
Ableitung
Regeln:
- Potenzregel:
- Funktion: f(x) = xz
- Ableitung: f'(x) = z ⋅ xz-1
- Faktorregel:
- Funktion: f(x) = c ⋅ g(x)
- Ableitung: f'(x) = c ⋅ g'(x)
- Summenregel:
- Funktion: f(x) = g(x) + h(x)
- Ableitung: f'(x) = g'(x) + h'(x)
- Wichtige Spezialfälle der Potenzregel:
- Funktion: f(x) = x
- Ableitung: f'(x) = 1
- Funktion g(x) = 1
- Ableitung: g'(x) = 0
Beispiel 1:

Beispiel 2:

Beispiel 3:

Änderungsdatum: 12.2.2020
Ableitung mit Kettenregel
Regeln:
- Kettenregel:
- Funktion: f(x) = u(v(x))
- Ableitung: f'(x) = v'(x) ⋅ u'(v(x))
- Sinusfunktion:
- Funktion: f(x) = sin(x)
- Ableitung: f'(x) = cos(x)
- Kosinusfunktion:
- Funktion: f(x) = cos(x)
- Ableitung: f'(x) = - sin(x)
- e-Funktion:
- Funktion: f(x) = ex
- Ableitung: f'(x) = ex
Beispiel 1:

Beispiel 2:
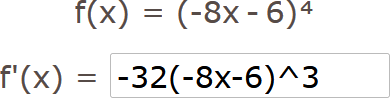
Beispiel 3:

Änderungsdatum: 12.2.2020
Ableitung mit Produktregel
Regeln:
- Produktregel:
- Funktion: f(x) = u(x) ⋅ v(x)
- Ableitung: f'(x) = u'(x) ⋅ v(x) + u(x) ⋅ v'(x)
- Sinusfunktion:
- Funktion: f(x) = sin(x)
- Ableitung: f'(x) = cos(x)
- Kosinusfunktion:
- Funktion: f(x) = cos(x)
- Ableitung: f'(x) = - sin(x)
- e-Funktion:
- Funktion: f(x) = ex
- Ableitung: f'(x) = ex
Beispiel 1:

Beispiel 2:

Änderungsdatum: 12.2.2020
Stammfunktion
Regeln:
- Potenzregel:
- Funktion: f(x) = xz
- Stammfunktion: F(x) = 1/(z+1) ⋅ xz+1
- Faktorregel:
- Funktion: f(x) = c ⋅ g(x)
- Stammfunktion: F(x) = c ⋅ G(x)
- Summenregel:
- Funktion: f(x) = g(x) + h(x)
- Stammfunktion: f(x) = G(x) + H(x)
- Wichtige Spezialfälle der Potenzregel:
- Funktion: f(x) = 1/x
- Stammfunktion: F(x) = ln(|x|)
- Funktion g(x) = 1
- Stammfunktion: G(x) = x
Beispiel 1:

Beispiel 2:

Beispiel 3:

Änderungsdatum: 12.2.2020
Stammfunktion mit linearer Verkettung
Regeln:
- Lineare Verkettung:
- Funktion: f(x) = g(cx + d)
- Stammfunktion: F(x) = 1/c ⋅ G(cx + d)
- Sinusfunktion:
- Funktion: f(x) = sin(x)
- Stammfunktion: F(x) = - cos(x)
- Kosinusfunktion:
- Funktion: f(x) = cos(x)
- Stammfunktion: F(x) = sin(x)
- e-Funktion:
- Funktion: f(x) = ex
- Stammfunktion: F(x) = ex
Beispiel 1:

Beispiel 2:
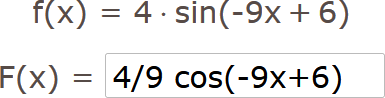
Beispiel 3:

Änderungsdatum: 12.2.2020
Programmierung: J. Merkert




